变换矩阵总结
摘要
变换矩阵 (Transformation Marices) 在图形学中的重要性不用多说,一切物体的缩放,旋转,位移,都可以通过变换矩阵作用得到。同时在投影 (projection) 变换的时候也有很多应用,本文将会介绍一些简要的变换矩阵。
1 2D线性变换
我们将如下图所示的简单矩阵乘法定义为对向量(x,y)T的线性变换。
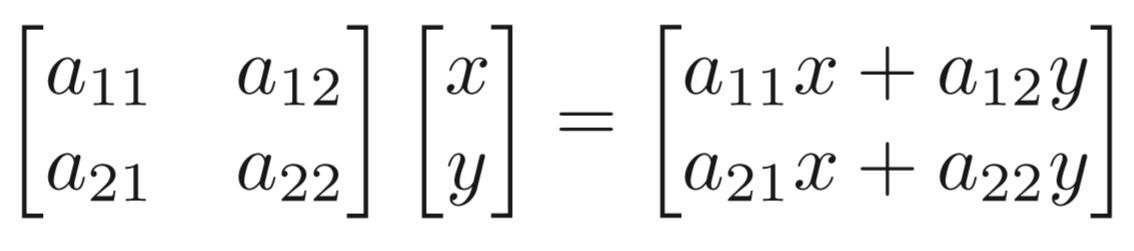
1.1 缩放(scaling)
缩放变换是一种沿着坐标轴作用的变换,定义如下:
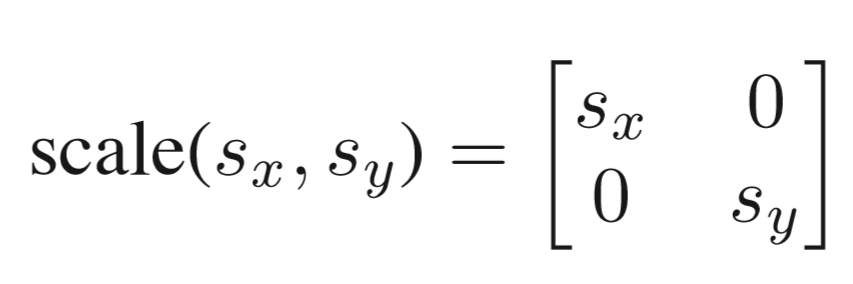
即除了(0,0)T保持不变之外,所有的点变为(sxx,syy)T。 举两个简单例子:
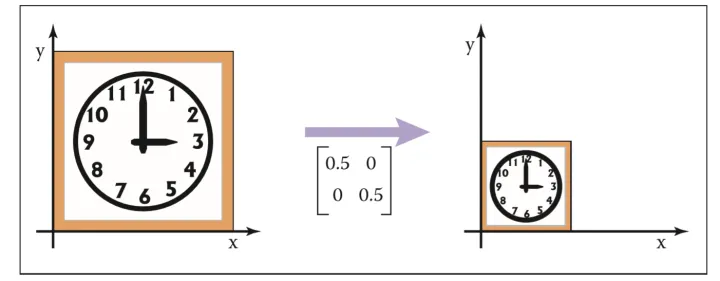
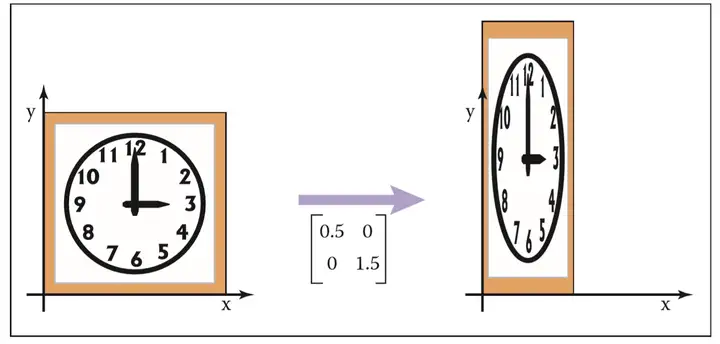
1.2 剪切(shearing)
shear变换直观理解就是把物体一边固定,然后拉另外一边,定义如下:
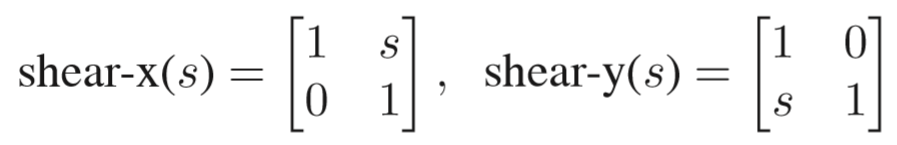
分别对应了向"拉伸"x轴,和"拉伸"y轴 直观理解见如下两图:
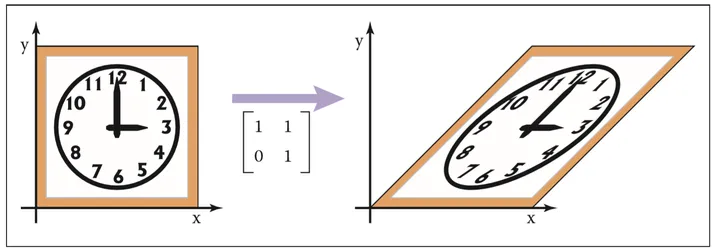
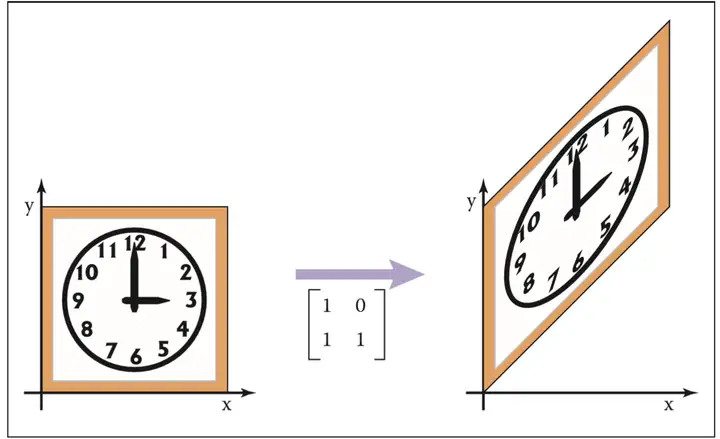
1.3 旋转(rotation)
旋转可以说是又一个十分重要的变换矩阵了,如下图,我们希望用一个变换矩阵表示将向量a旋转到向量b的位置,
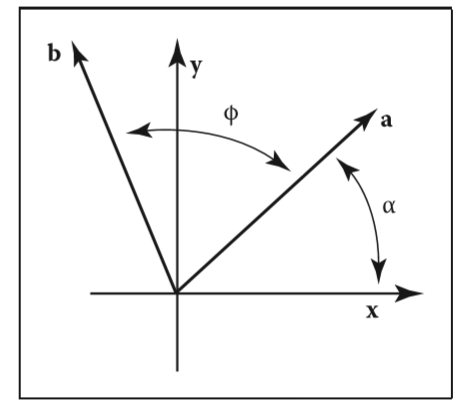
记为
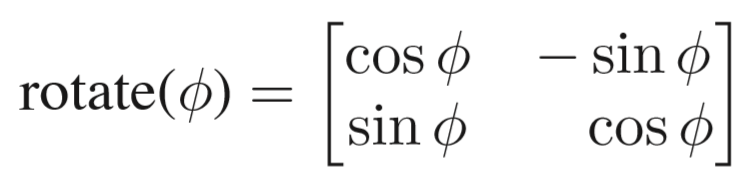
我们可做如下推导得到该矩阵,记向量长度为r,则不难得到
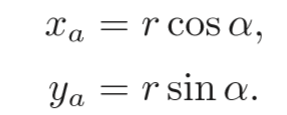
进一步我们可以将旋转之后的向量b的坐标x,y用如下表示

显然,将上一步xa和ya的坐标表示代入得到

此时不难得出该结果即为rotate(ϕ)∗(xa,ya)T的结果了,证明结束。(注意该式是逆时针(countercklockwise)旋转,且原点为旋转中心!)
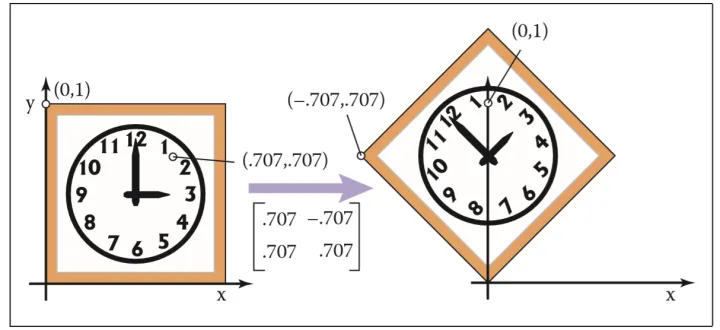
举例逆时针旋转45°效果如下:
2 3D线性变换
其实知道2维推3维还是非常直观的,只有推3维旋转的时候有一点要注意一下。
2.1 3维缩放(scaling),剪切(shearing),旋转(rotation)
缩放不用多说:
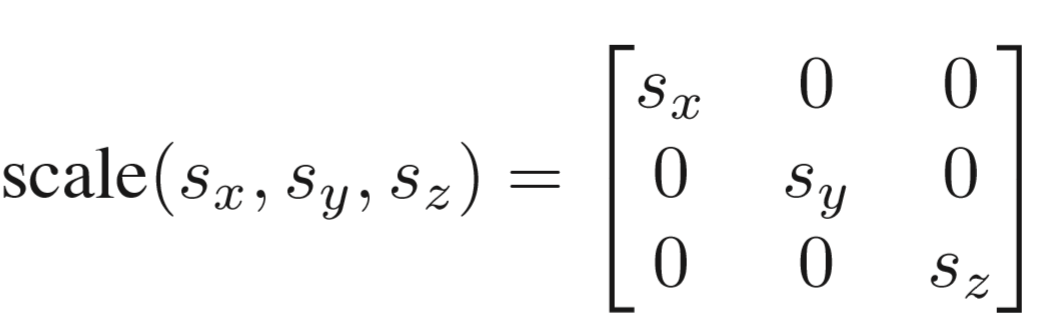
剪切也十分类似:
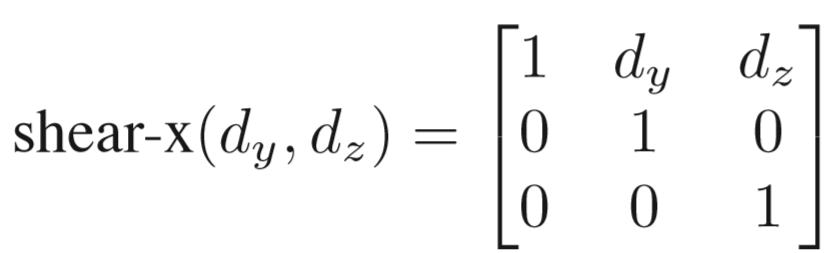
对于3维旋转来说一共有3类矩阵,分别对应绕x轴,y轴,z轴旋转,同时有很关键的一点要注意!我们所采用的是右手系,所以在二维之中其逆时针旋转矩阵是x轴向y轴旋转,对应到3维便是绕z轴旋转(x轴转向y轴),不难推出绕x轴旋转(y转向z),绕y轴旋转(z转向x), 如果想不明白,右手螺旋定则试一试就知道了! x->y->z->x......
因此理解了上面这点,对应二维旋转矩阵能够类推得到三维旋转矩阵如下:
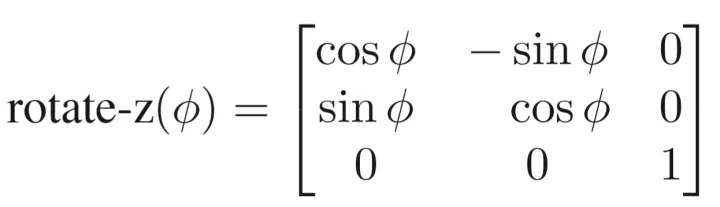
(绕z轴,故z不变,且x转向y,左上角与二维逆时针旋转矩阵相同)
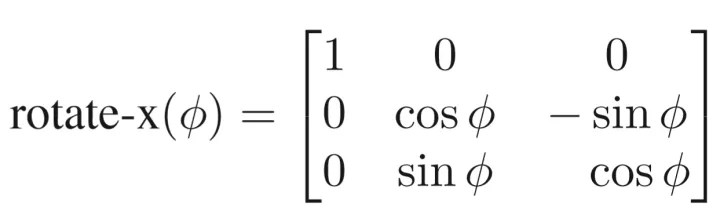
(绕x轴,故x不变,且y转向z,右下角与二维逆时针旋转矩阵相同)
绕y轴会有一点不同,但只要记住需要z转向x,很快便能反应过来
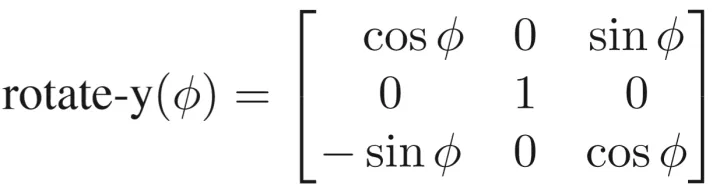
其实到这里可以下一个结论,可以看到任意旋转都是正交矩阵!,因此他们的逆便是他们的转置,而一个旋转矩阵的逆所对应的几何解释便是,我反着转这么多,比如我逆时针转30°,转置便是顺时针30°
注:以上所有的旋转都是针对原点来说,那么如何对围绕任何一个轴(3维)旋转呢
2.2 3维绕任意轴旋转
我们只有绕x,y, z旋转的方法,怎么随便给一个轴让你绕着他旋转呢!很直观的,先把该轴给先旋转到x或者y或者z轴上,接着就可以应用上面已经得到的标准旋转矩阵,最后要记得把该轴逆旋转回它原先的地方就完成了,用矩阵表示如下:
R1RxR1T∗(x,y,z)T
这里的Rx是知道的,也就是3维下绕x轴旋转的矩阵,那么根据之前的分析问题只剩怎么求R1了,设我们想围绕旋转的轴为u,R1便是将u旋转到x的矩阵。 具体来说这里需要以u为一轴,构造一个3维正交坐标系,然后将u-x对齐,那么其它两轴就肯定和y和z对齐了!
构造如下,任取一t方向不与u重合
w = t x u
v = u x w
此时u, w, v便是我们构造出的新坐标系(这里运用了一些叉乘的几何性质)。
好了,现在得到了u,w,v 对应 x,y,z如何将我们的新坐标系与原始坐标系重合呢,这其实很简单,直接取R1 = (u,w,v), 该旋转矩阵的含义便是将x,y,z旋转到u,w,v的旋转矩阵(读者可以直接计算R1 x,R1 *y,R1 ** z试试便一目了然)。
还记得什么?在上一节曾总结到,旋转矩阵是正交矩阵,旋转矩阵的转置便是它的逆,也是几何意义上的反作用,因此!RT便是将u,w,v旋转到x,y,z的矩阵了。现在我们知道了R1知道了RX,那么围绕任意轴的旋转也就得到了!
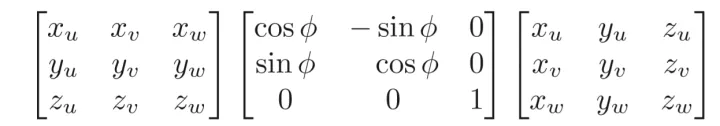
中间那个矩阵换成 rotate−x(ϕ)就好啦!截图没有改
Tips:如果读者对线性代数不熟悉,或是没有很直观的几何理解的话,强烈推荐3blue1brown的线代本质.真的是带你走进全新版本。
3 仿射变换
其实读到这大部分矩阵变换都已经说完了,只剩最后一个位移,同时也会引入齐次坐标为了更好将位移与rotation,scaling结合再一起,这样能够有旋转scale,又有translation的变换,称之为仿射变换。
3.1 位移(translation)
其实位移是在简单不过的了
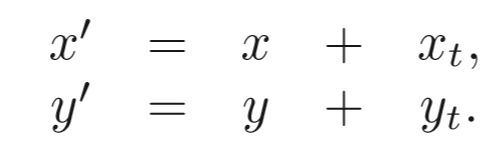
我们之前所提到的线性变换如下:
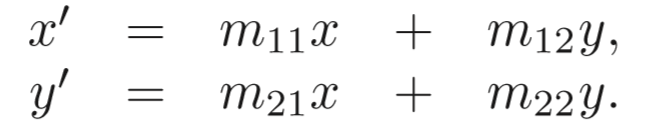
你可以试试如果2维变换只用2维矩阵,3维变换只用3维矩阵,你是不可能将二者合在一起用一个矩阵表示的,所以很自然的,我们引入一维新的坐标,称之为齐次坐标,(x,y)->(x,y,1)
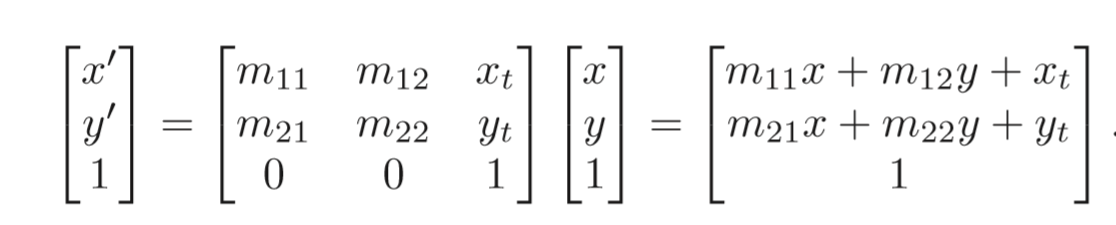
现在我们就可以用一个矩阵即表示线性变换,又表示位移了!三维其实同理,完全一样,不过有点要注意的是,对于带有齐次坐标的变换,会先进行线性变换(即scale,rotation,shear这些),之后才会进行位移!
注:最后一维为1,表示点(point), 为0表示方向(direction).方向的位移没有意义,方向始终不会变。 当然,第四维不是只能是1和0,在投影变换中,齐次坐标会有更多的作用。
Reference
[1] Fundamentals of Computer Graphics 4th